Quorum intersection despite $B$

This protects against nodes in $B$ making contradictory assertions that enable other nodes to externalize inconsistent values for the same slot. If $\ev{V, Q}^B$ enjoys quorum intersection but does not enjoy quorum availability despite $B$, then $\ev{V, Q}$ will have a problem when nodes in $B$ start making contradictory assertions.

In the following example, $\ev{V, Q}^B$ enjoys quorum intersection because any quorum in $\ev{V, Q}^B$ must contain at least two of $v_4, v_5, v_6$. On the other hand, $V \setminus B$ is not a quorum.

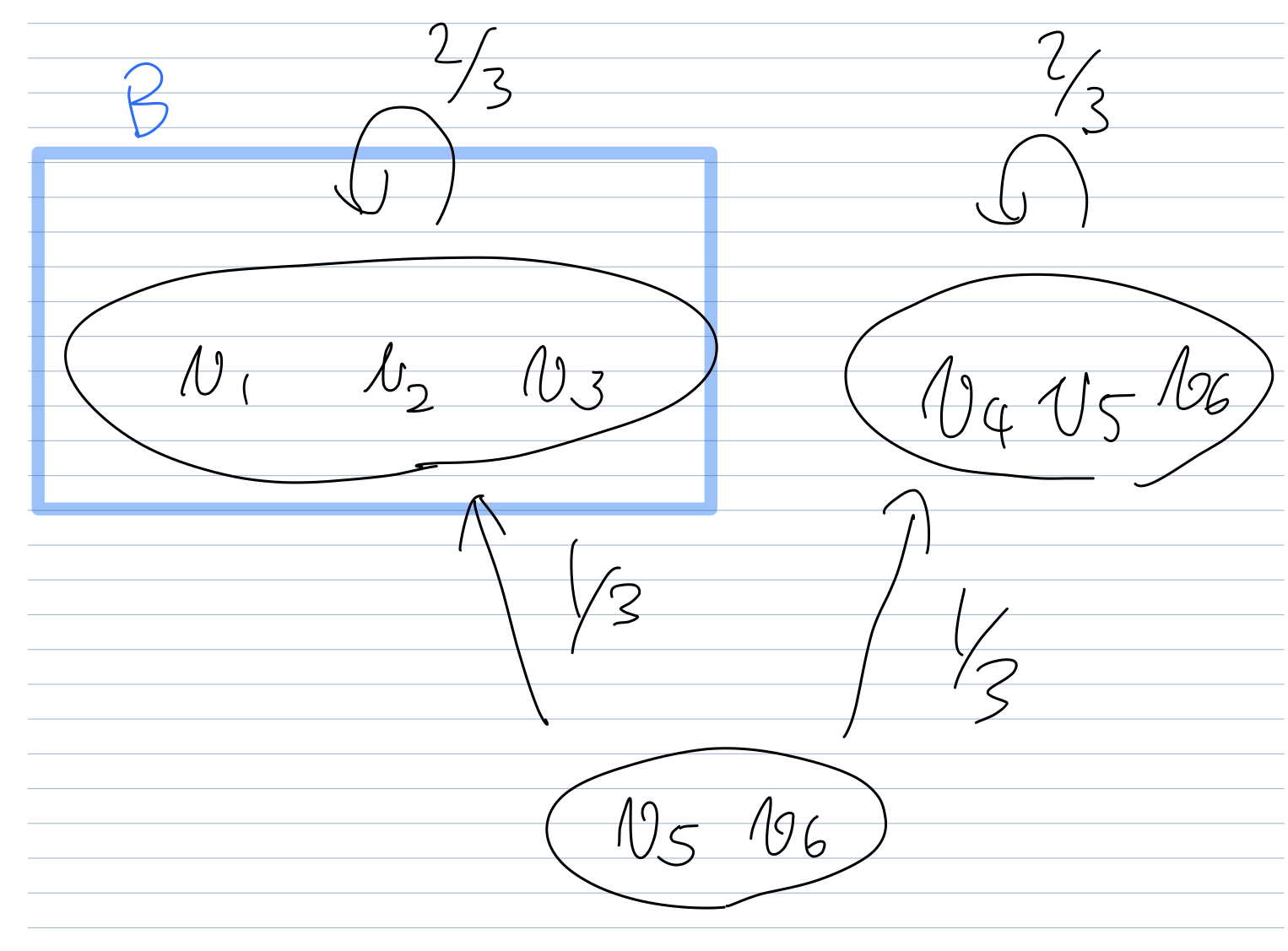
Quorum availability despite $B$

This protects against nodes in $B$ refusing to answer requests and blocking other nodes’ progress. Suppose $\ev{V, Q}^B$ does not enjoy quorum intersection but enjoys quorum availability despite $B$.

Consider the FBAS in the DSet example post. Let $B = \{ v_5, v_6 \}$. Then $V \setminus B$ is indeed a quorum. As shown in the first proposition in the DSet example post, $B$ does not enjoy quorum intersection.