We will prove some of the claims made on P.9-10 of the Stellar white paper.

Proposition

The smallest DSet containing $v_5, v_6$ in Figure 3 below is $\{ v_5, v_6, v_9, v_{10} \}$.

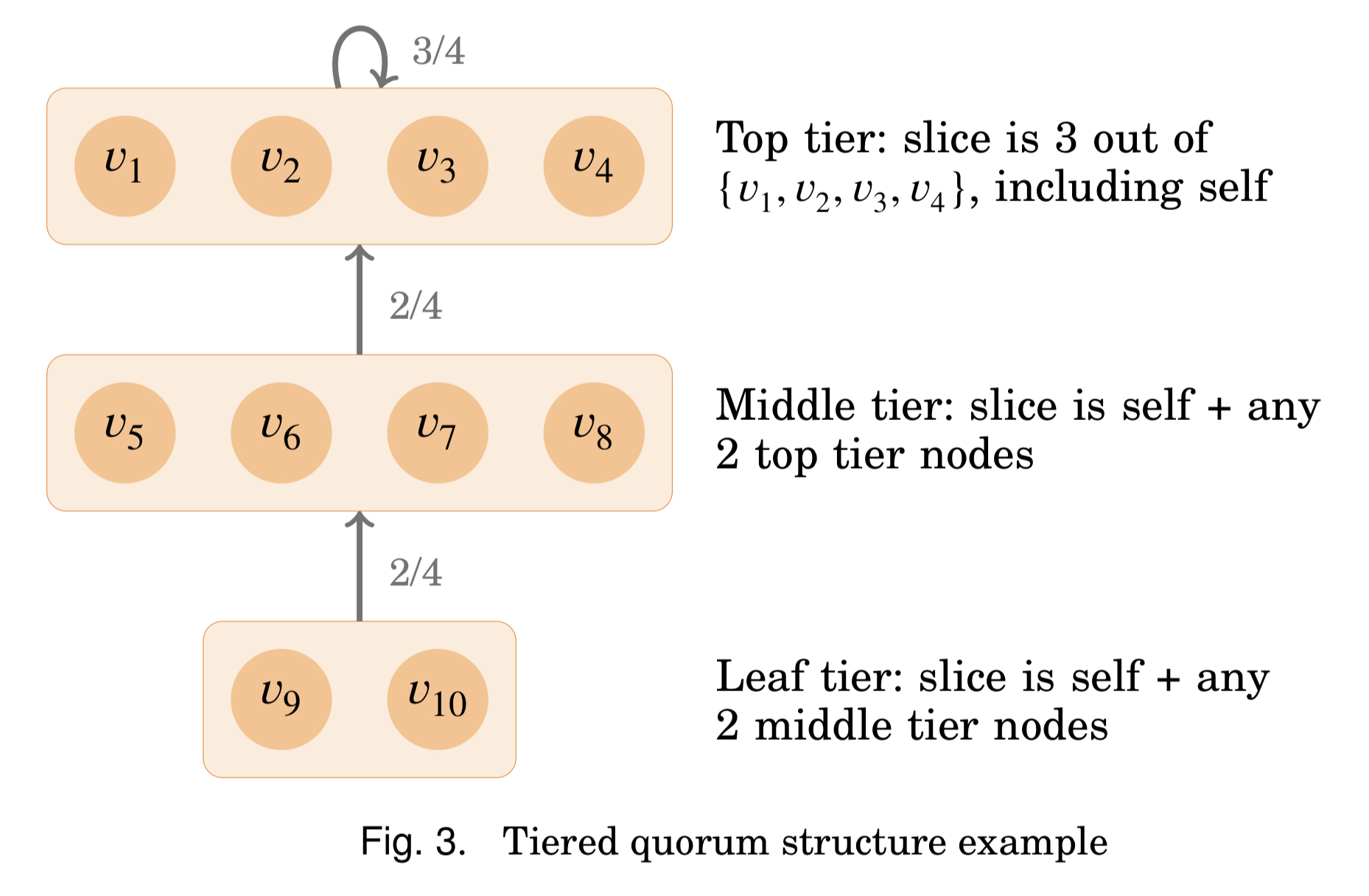
Proof

First, we will show that $B = \{ v_5, v_6 \}$ is not a DSet. By definition, $Q^B(v_9) = \{ \{ v_9 \}, \{ v_9, v_7 \}, \{ v_9, v_8 \}, \{ v_9, v_7, v_8 \} \}$. Similarly, $Q^B(v_{10}) = \{ \{ v_{10} \}, \{ v_{10}, v_7 \}, \{ v_{10}, v_8 \}, \{ v_{10}, v_7, v_8 \} \}$. This implies that $U = \{ v_9 \}$ and $V = \{ v_{10} \}$ are both quorums. Then $U \cap V = \emptyset$, so $\ev{V, Q}^B$ does not enjoy quorum intersection. Therefore, $B$ is not a DSet.

Next, we will consider $C = \{ v_5, v_6, v_1 \}$. Then we can use the same argument as above. $U = \{ v_9 \} \in Q^C(v_9)$ and $V = \{ v_{10} \} \in Q^C(v_{10})$, and the intersection is empty. Therefore, $C$ is not a DSet. It is easy to see that this argument works for the case of $\{ v_5, v_6, v_i \}$ for any $i = 1, 2, 3, 4$.

We will consider $D = \{ v_5, v_6, v_9 \}$. Similarly, $U = \{ v_{10} \} \in Q^D(v_{10})$ is a quorum. Moreover, $V = \{ v_1, v_2, v_3, v_4 \}$ is a quorum. Then $U \cap V = \emptyset$, so $\ev{V, Q}^D$ does not enjoy quorum intersection. It is easy to see that a similar argument shows that $\{ v_5, v_6, v_{10} \}$ is not a DSet.

Finally, we will show that $E = \{ v_5, v_6, v_9, v_{10} \}$ is a DSet. $V \setminus E$ is a quorum because every quorum slice of every node in $V \setminus E$ only contain nodes in $V \setminus E$. Any quorum in $\ev{V, Q}^E$ contain at least three of $v_1, v_2, v_3, v_4$ because $v_1, v_2, v_3, v_4$ need at least three of them and $v_5, v_6$ need at least two of them. Therefore, any intersection contains at least two of $v_1, v_2, v_3, v_4$ by the pigeon hole principle.

Therefore, $E$ is indeed a smallest DSet containing $v_5$ and $v_6$.

Proposition

$B = \{ v_1 \}$ is a DSet.

Proof

First, we will check if $\ev{V, Q}$ enjoys quorum intersection despite $B$.

Consider $\ev{V, Q}^B$. Any quorum containing $v_9$ and/or $v_{10}$ must contain at least two of $v_5, v_6, v_7, v_8$. Any quorum containing at least one of $v_5, \cdots, v_8$ must contain at least one of $v_2, v_3, v_4$. Any quorum containing at least one of $v_2, v_3, v_4$ must contain at least two of $v_2, v_3, v_4$. This is because $Q(v_i)^B = \{ \{ v_2, v_3, v_4 \}, \{ v_i, v_j \}, \{ v_i, v_k \} \}$ where $\{ i, j, k \} = \{ 2, 3, 4 \}$.

Therefore, the intersection of any two quorums must contain at least one of $v_2, v_3, v_4$ by the pigeon hole principle.

Next, we need to check if $\ev{V, Q}$ enjoys quorum availability despite $B$. $V \setminus B$ is indeed a quorum in $\ev{V, Q}$ because each node in $V \setminus B$ has a quorum slice that doesn’t contain $v_1$.