An application of the universal property of a tensor product
by Hidenori
Proposition
Let $A, B$ be rings, let $M$ be an $A$-module, $P$ a $B$-module, and $N$ an $(A, B)$-bimodule. Then $M \otimes_A N$ is naturally a $B$-module, $N \otimes_B P$ an $A$-module, and we have
\[\begin{align*} (M \otimes_A N) \otimes_B P \cong M \otimes_A (N \otimes_B P). \end{align*}\]Solution
We will check if $(M \otimes_A N) \otimes_B P$ and $M \otimes_A (N \otimes_B P)$ are isomorphic as $A$-modules and $B$-modules.
Let $z \in P$ be fixed. Construct an $A$-bilinear map $f_z: M \times N \rightarrow M \otimes_A (N \otimes_B P)$ such that $f_z(x, y) = x \otimes (y \otimes z)$.
$f_z$ is $A$-bilinear because
\[\begin{align*} f_z(ax + x', y) &= (ax + x') \otimes (y \otimes z) \\ &= ax \otimes (y \otimes z) + x' \otimes (y \otimes z) \\ &= a(x \otimes (y \otimes z)) + x' \otimes (y \otimes z) \\ &= af_z(x, y) + f_z(x', y), \end{align*}\]and
\[\begin{align*} f_z(x, ay + y') &= x \otimes ((ay + y') \otimes z) \\ &= x \otimes ((ay \otimes z) + (y' \otimes z)) \\ &= (x \otimes a(y \otimes z)) + x \otimes (y \otimes z) \\ &= a(x \otimes (y \otimes z)) + x \otimes (y \otimes z) \\ &= af_z(x, y) + f_z(x, y'). \end{align*}\]By the universal property of a tensor product, there exists a unique $A$-linear map $\tilde{f}_z$ such that the following diagram commutes:
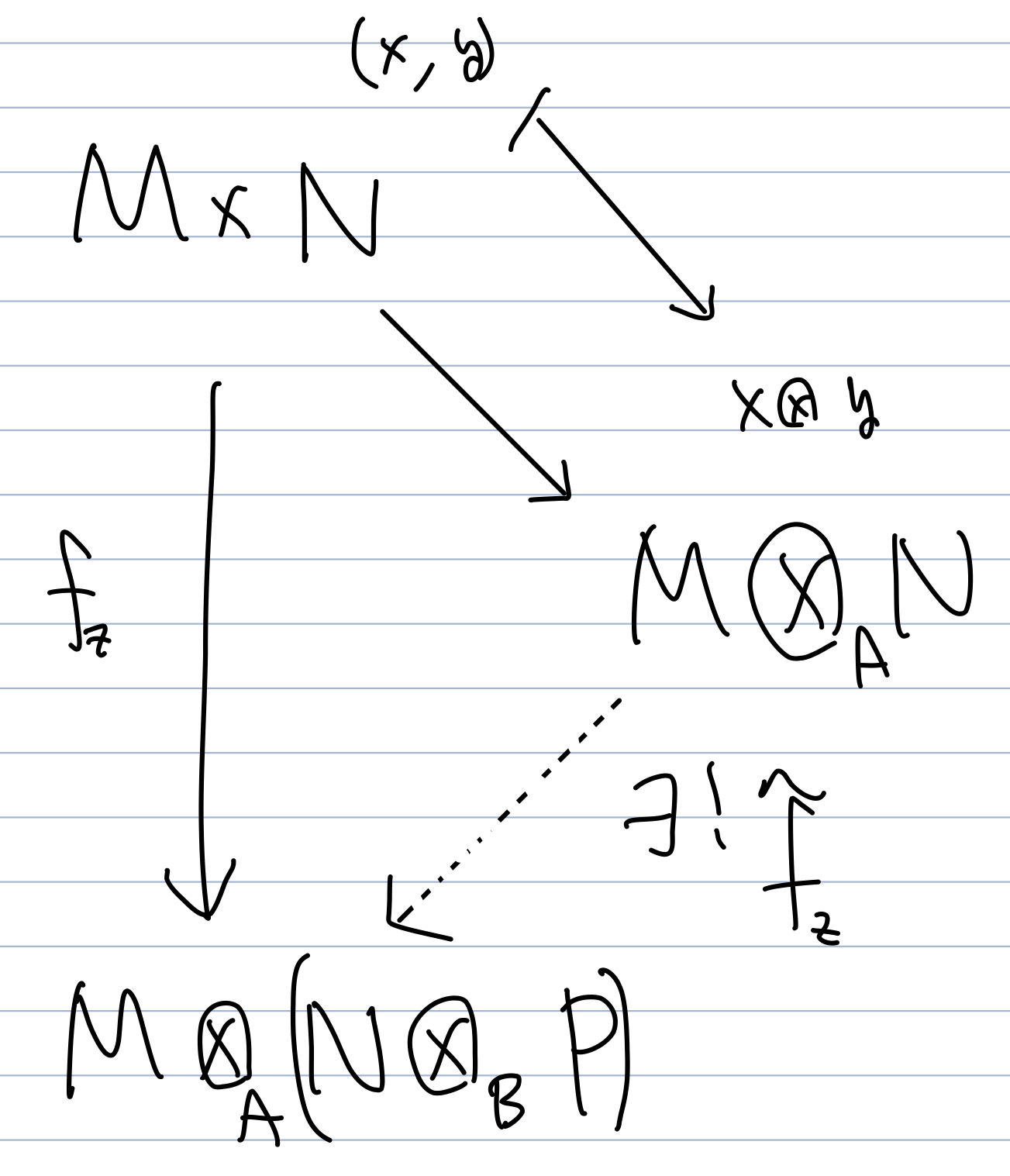
Since the diagram above commutes and $\tilde{f}_z$ is $A$-linear, \(\tilde{f}_z(\sum_{i=1}^{n} x_i \otimes y_i) = \sum_{i=1}^{n} (x_i \otimes (y_i \otimes z))\). $\tilde{f}_z$ is also $B$-linear because
\[\begin{align*} \tilde{f}_z(b(\sum x_i \otimes y_i) + (\sum x'_j \otimes y'_j)) &= \tilde{f}_z((\sum x_i \otimes by_i) + (\sum x'_j \otimes y'_j)) \\ &= \sum (x_i \otimes (by_i \otimes z)) + \sum (x'_j \otimes (y'_j \otimes z)) \\ &= \sum (x_i \otimes b(y_i \otimes z)) + \sum (x'_j \otimes (y'_j \otimes z)) \\ &= b\sum (x_i \otimes (y_i \otimes z)) + \sum (x'_j \otimes (y'_j \otimes z)) \\ &= b\tilde{f}_z(\sum x_i \otimes y_i) + \tilde{f}_z(\sum x'_j \otimes y'_j). \end{align*}\]This argument works for any $z \in P$.
Let $f: (M \otimes_A N) \times P \rightarrow M \otimes_A (N \otimes_B P)$ be defined such that $f(\sum x_i \otimes y_i, z) = \tilde{f}_z(\sum x_i \otimes y_i)$. $f$ is a $B$-bilinear map becasue
\[\begin{align*} f(b\sum x_i \otimes y_i + \sum x'_i \otimes y'_i, z) &= f(\sum x_i \otimes by_i + \sum x'_i \otimes y'_i, z) \\ &= \tilde{f}_z(\sum x_i \otimes by_i + \sum x'_i \otimes y'_i ) \\ &= \sum x_i \otimes (by_i \otimes z) + \sum x'_i \otimes (y'_i \otimes z) \\ &= \sum x_i \otimes b(y_i \otimes z) + \sum x'_i \otimes (y'_i \otimes z) \\ &= b(\sum x_i \otimes (y_i \otimes z)) + \sum x'_i \otimes (y'_i \otimes z) \\ &= bf(\sum x_i \otimes y_i) + f(\sum x'_i \otimes y'_i). \end{align*}\]By the universal property of a tensor product, there exists a unique $B$-linear map $\tilde{f}$ such that the following diagram commutes:
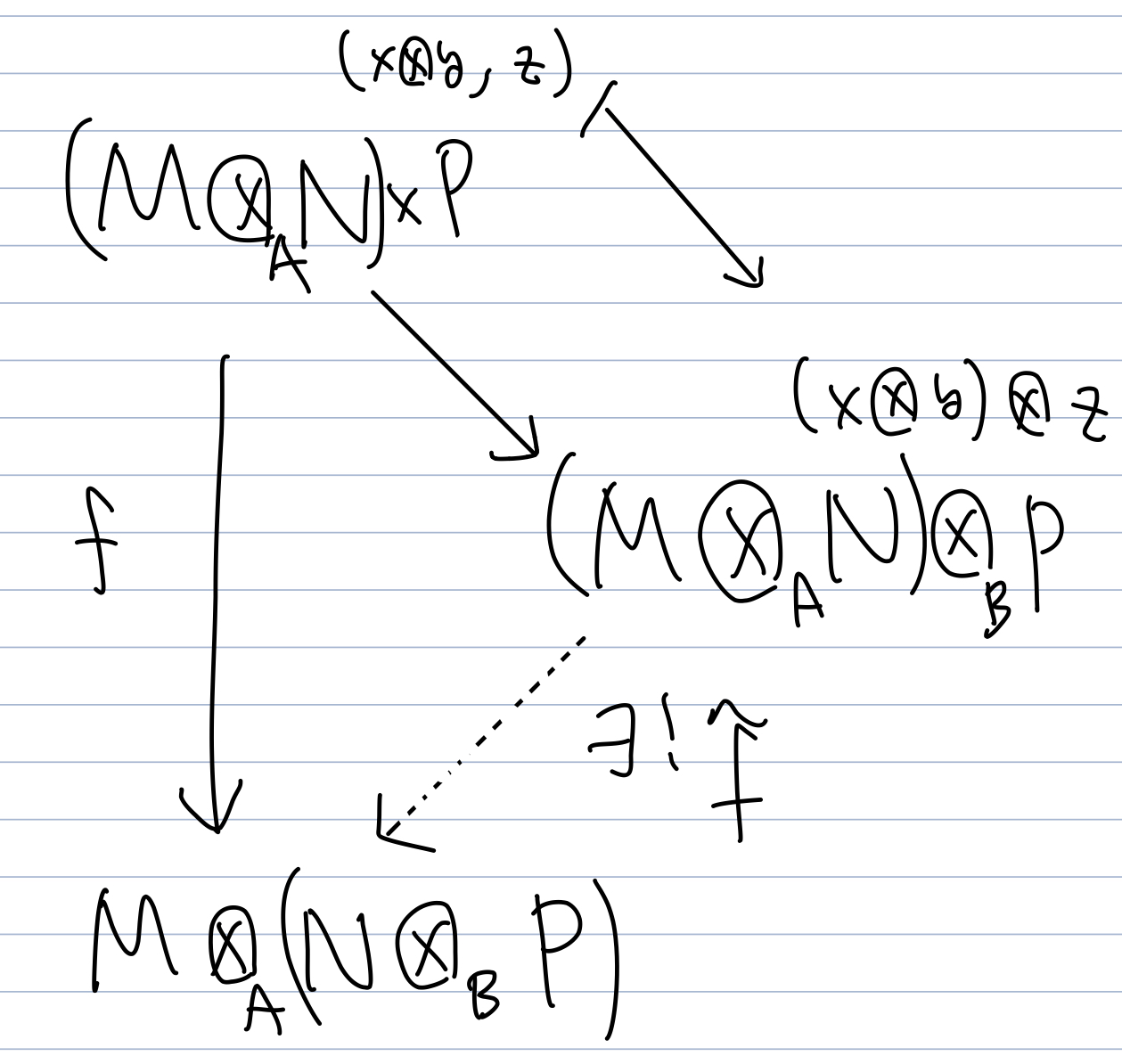
Based on the diagram and the fact that $\tilde{f}$ is $B$-linear, \(\tilde{f}(\sum_i (\sum_j x_{i, j} \otimes y_{i, j}) \otimes z_i) = \sum_i (\sum_j x_{i, j} \otimes (y_{i, j} \otimes z_{i}))\). For simplicity, we will just write $\tilde{f}((x \otimes y) \otimes z) = x \otimes (y \otimes z)$ because there exists exactly one $B$-linear map that satisfies this. Moreover, it is easy to see that $\tilde{f}$ is $A$-linear.
A similar argument shows that the inverse map of $f$ is both $A$-linear and $B$-linear, so $f$ is both an $A$-module isomorphism and $B$-module isomorphism.
Subscribe via RSS
