Proposition

If $M$ is a $k$-dimensional manifold-with-boundary, prove that $\partial M$ is a $(k - 1)$-dimensional manifold and $M \setminus \partial M$ is a $k$-dimensional manifold.

Solution

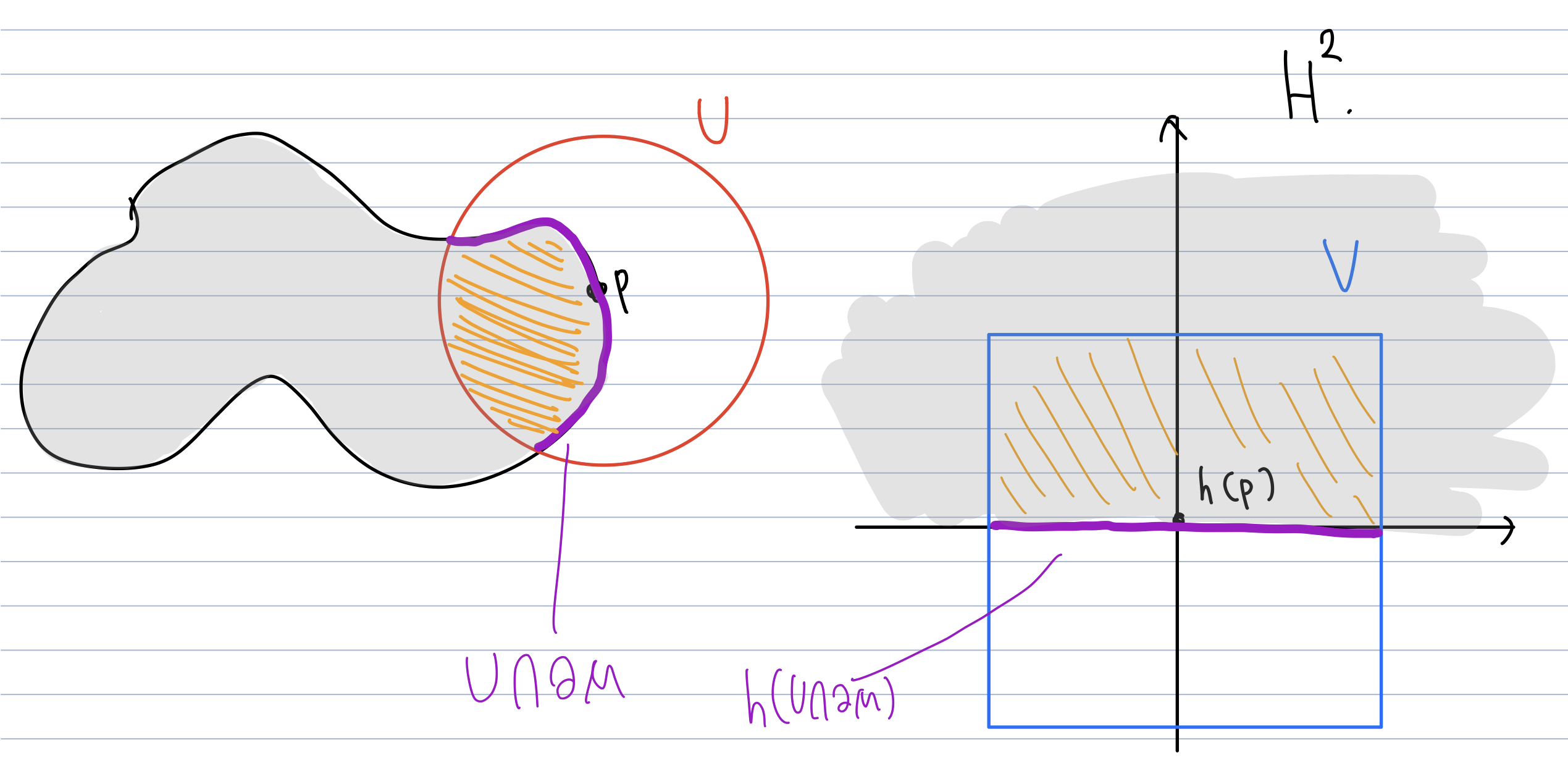
Let $p \in \partial M$. Then there exists an open subset $U$ containing $p$ and an open subset $V \subset \mathbb{R}^n$ with a diffeomorphism $h: U \rightarrow V$ such that $h(U \cap M) = V \cap (\mathbb{H}^k \times \{ 0 \})$.

Let $q \in U \cap \partial M$. Suppose that the $k$th coordinate of $h(q)$ is $> 0$. Then we can take a neighborhood of $q$ that is contained in $U$, then the point $q$ satisfies the condition to be a part of a manifold (This condition is denoted as (M) in Spivak). However, as mentioned on P.113[Spivak], the conditions (M) and (M’) cannot be both satisfied by the same point. Therefore such a $q$ does not exist.

On the other hand, let $q \in U \cap (M \setminus \partial M)$. If the $k$th coordinate of $h(q)$ is 0, then $q$ satisfies the condition (M’). Again, this is impossible for the same reason as above.

Therefore, the $k$th coordinate is 0 if and only if the point is in the boundary. Since $h$ is a diffeomorphism, $h(U \cap \partial M) = V \cap (\mathbb{H}^k \times \{ 0 \}) \cap \mathbb{R}^{k - 1} = V \cap \mathbb{R}^{k - 1}$.

Therefore, $\partial M$ is a $(k - 1)$-dimensional manifold.

Let $p \in (M \setminus \partial M)$. Then there exists an open subset $U$ containing $p$ and an open subset $V \subset \mathbb{R}^n$ with a diffeomorphism $h: U \rightarrow V$ such that $h(U \cap M) = V \cap (\mathbb{R}^k \times \{ 0 \})$. $U \cap M$ and $U \cap \partial M$ must be disjoint because any point in the intersection would satisfy the two conditions (M) and (M’). Therefore, $h(U \cap (M \setminus \partial M)) = h(U \cap M)$ and thus $M \setminus \partial M$ is a $k$-dimensional manifold.