Proposition

Find the length of the following paths:

1. $\gamma(t) = 3t + i, -1 \leq t \leq 1$.
2. $\gamma(t) = i + e^{i\pi t}, 0 \leq t \leq 1$.
3. $\gamma(t) = i\sin(t), -\pi \leq t \leq \pi$.
4. $\gamma(t) = t - ie^{-it}, 0 \leq t \leq 2\pi$.

Solution

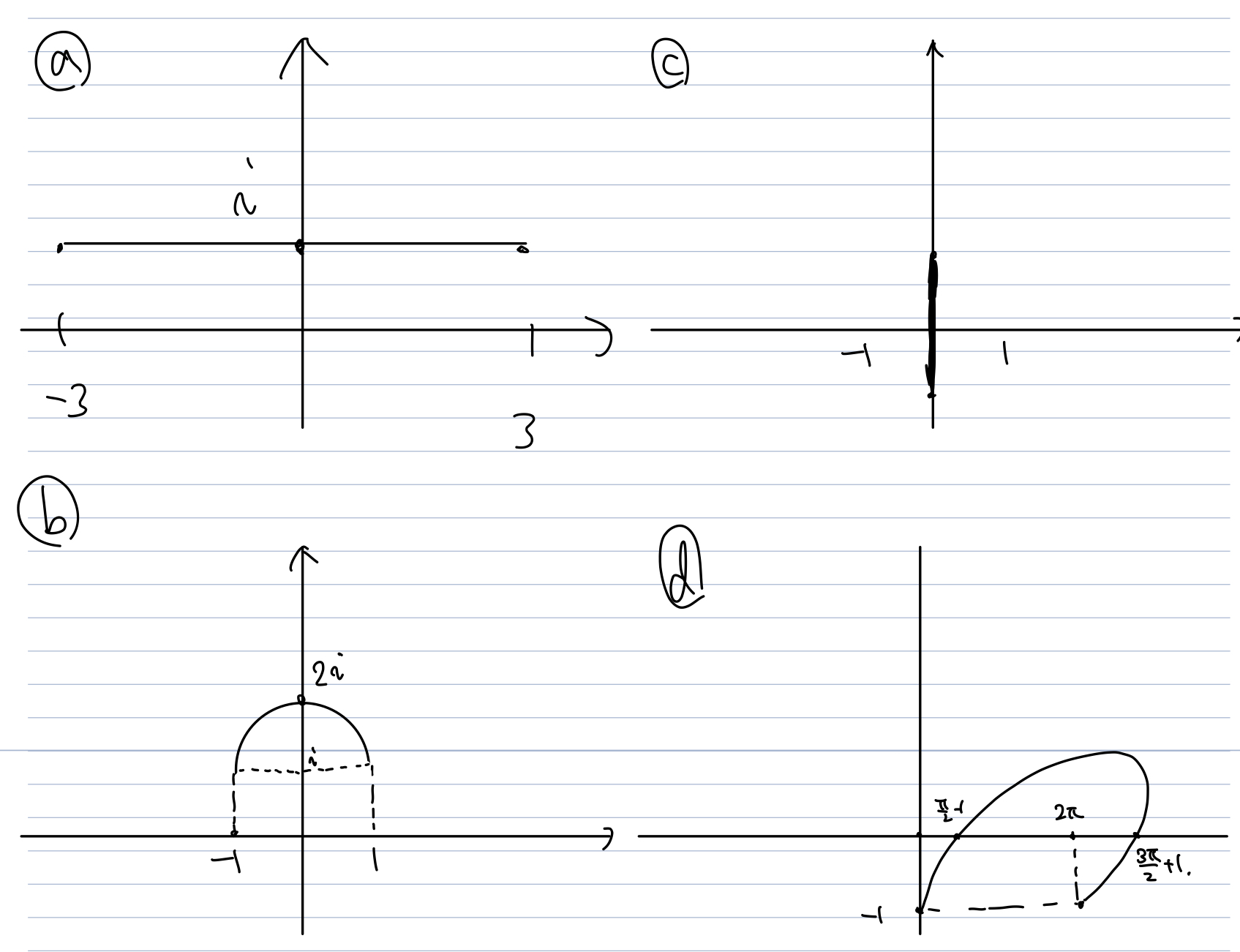
1

$\int_{-1}^{1} \abs{\gamma’(t)}dt = \int_{-1}^{1} 3dt = 6$.

2

$\int_{0}^{1} \abs{\gamma’(t)}dt = \int_{0}^{1} \pi dt = \pi$.

3

$\int_{-\pi}^{\pi} \abs{\gamma’(t)}dt = \int_{-\pi}^{\pi} \cos(t) dt = 4\int_{0}^{\pi/2} \cos(t)dt = 4$.

4

$\int_{0}^{2\pi} \abs{\gamma’(t)}dt = \int_{0}^{2\pi} \abs{1 - e^{-it}} dt = \int_{0}^{2\pi} \abs{2 - 2\cos t} dt = 8$. (I’m not sure how to integrate this, but this is what Wolfram Alpha says.)