Proposition

1. Any composition of quotient maps is a quotient map.
2. An injective quotient map is a homeomorphism.
3. If $q: X \rightarrow Y$ is a quotient map, a subset $K \subset Y$ is closed if and only if $q^{-1}(K)$ is closed in $X$.
4. If $q: X \rightarrow Y$ is a quotient map and $U \subset X$ is a saturated open or closed subset, then the restriction $q \mid_{U}: U \rightarrow q(U)$ is a quotient map.
5. TODO

Solution

1

Let $X, Y, Z$ be topological spaces and $p: X \rightarrow Y, q: Y \rightarrow Z$ be quotient maps. Let $U \subset Z$ be given.

• Since $q$ is a quotient map, $U$ is open if and only if $q^{-1}(U)$ is open.
• Since $p$ is a quotient map, $q^{-1}(U)$ is open if and only if $p^{-1}(q^{-1}(U))$ is open.

Therefore, $U$ is open if and only if $p^{-1}(q^{-1}(U))$ is open. Since $p^{-1}(q^{-1}(U)) = (q \circ p)^{-1}(U)$, $U$ is open if and only if $(q \circ p)^{-1}(U)$ is open. Therefore, $q \circ p$ is a quotient map.

2

Let $q: X \rightarrow Y$ be an injective quotient map.

• $q$ is injective.
• Since $q$ is a quotient map, $q$ is surjective.
• Since $q$ is a quotient map, $q$ is continuous.
• Let $U \subset X$ be an open set. Then $U = q^{-1}(q(U))$ because $q$ is injective. Since $q$ is a quotient map, $q(U)$ must be open. Therefore, $q$ is an open map.

Therefore, $q$ is bijective, continuous, and open, so it is indeed a homeomorphism.

3

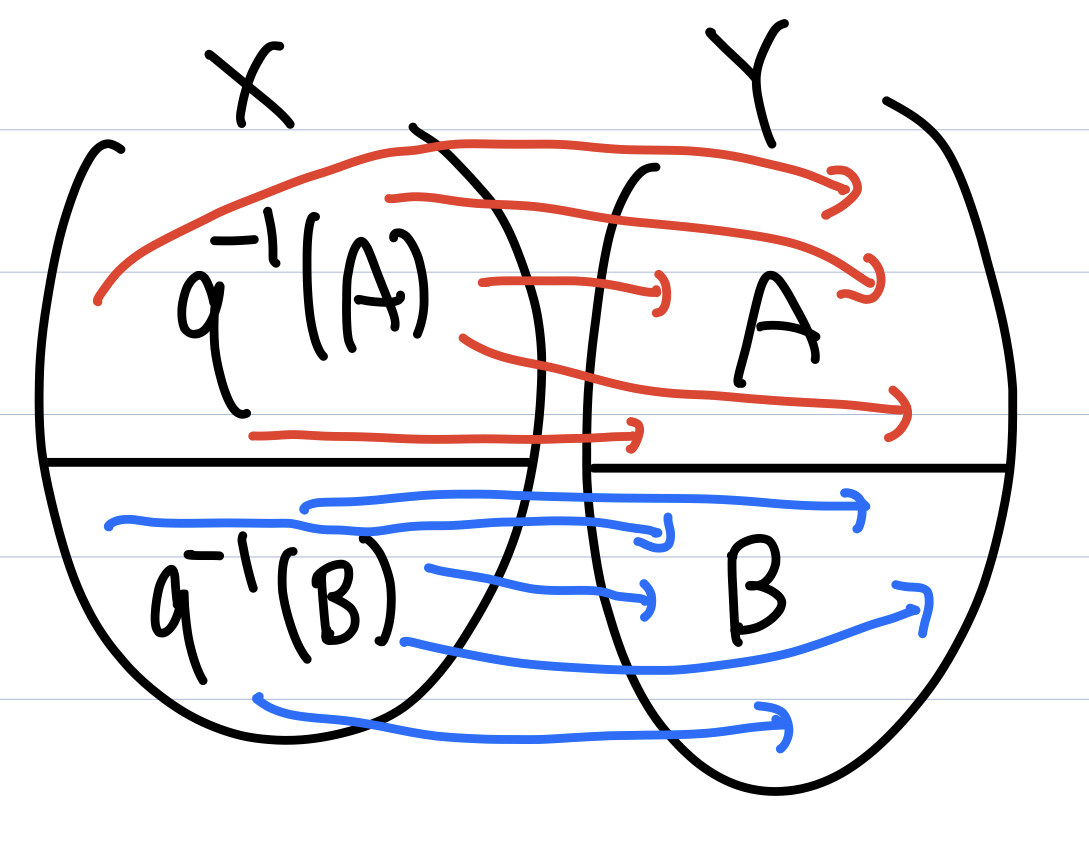The idea is that if $Y = A \cup B$ and $A \cap B = \emptyset$, $X = q^{-1}(A) \cup q^{-1}(B)$ and $q^{-1}(A) \cap q^{-1}(B) = \emptyset$. Therefore, $A$ is closed $\iff$ $B$ is open $\iff$ $q^{-1}(B)$ is open $\iff$ $q^{-1}(A)$ is closed.

Suppose $q: X \rightarrow Y$ is a quotient map. Let $K \subset Y$ be given.

Suppose $K$ is closed in $Y$. Then $Y \setminus K$ is open. Since $q$ is a quotient map, $q^{-1}(Y \setminus K)$ is open. Therefore, $X \setminus q^{-1}(K)$ is open, so $q^{-1}(K)$ is closed.

On the contrary, suppose that $q^{-1}(K)$ is closed. Then $X \setminus q^{-1}(K)$ is open. This implies that $q^{-1}(Y \setminus K)$ is open. Since $q$ is a quotient map, $Y \setminus K$ is open. Therefore, $K$ is closed.

4

Let $U \subset X$ be a saturated open subset. Let $V \subset Y$ be given such that $q^{-1}(V) = U$. Since $q$ is a quotient map, $V$ must be open in $Y$.

Since $q$ is continuous, the restriction $q \mid_U$ is continuous. Let $W \subset V$ be given. Since $W \subset V = q(U)$, $q^{-1}(W) \subset q^{-1}(V) = q^{-1}(q(U)) \subset U$. Therefore, $q^{-1}(W) \subset U$, so $(q\mid_U)^{-1}(W) = q^{-1}(W)$.

Suppose that $(q\mid_U)^{-1}(W)$ is open in $U$. Since $U$ is open and $q^{-1}(W) = (q\mid_U)^{-1}(W)$, $q^{-1}(W)$ is open in $X$. Since $q$ is a quotient map, $W$ is open in $Y$. Therefore, $W$ is open in $V$, so $q\mid_U$ is indeed a quotient map.

TODO

5

TODO