Proposition

Every continuous map $h: D^2 \rightarrow D^2$ has a fixed point, that is, a point $x \in D^2$ with $h(x) = x$.

Solution

Suppose that $h(x) \ne x$ for any $x \in D^2 = \{ x \in \mathbb{R}^2 \mid \abs{x} \leq 1 \}$.

Define $r: D^2 \rightarrow S^1$ as following:

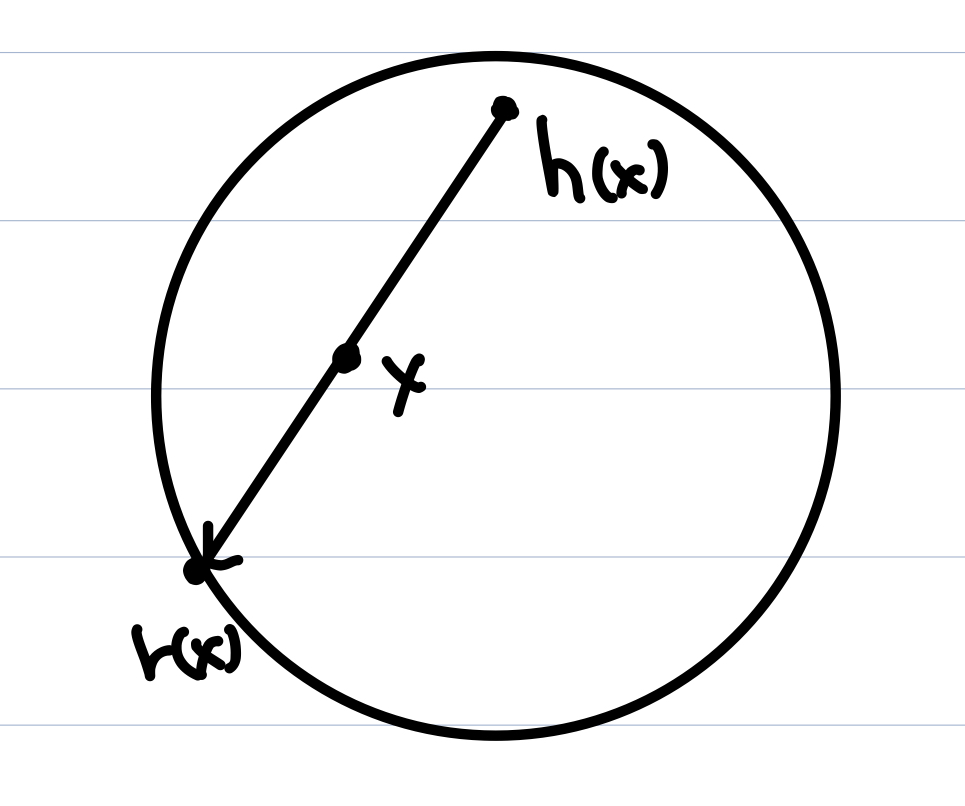
We claim that $r(x)$ is continuous. Let $x \in D^2$ be given. Let $\epsilon > 0$ be given. We claim the existence of a $\delta > 0$ such that $r(N(x, \delta)) \subset N(r(x), \epsilon)$.

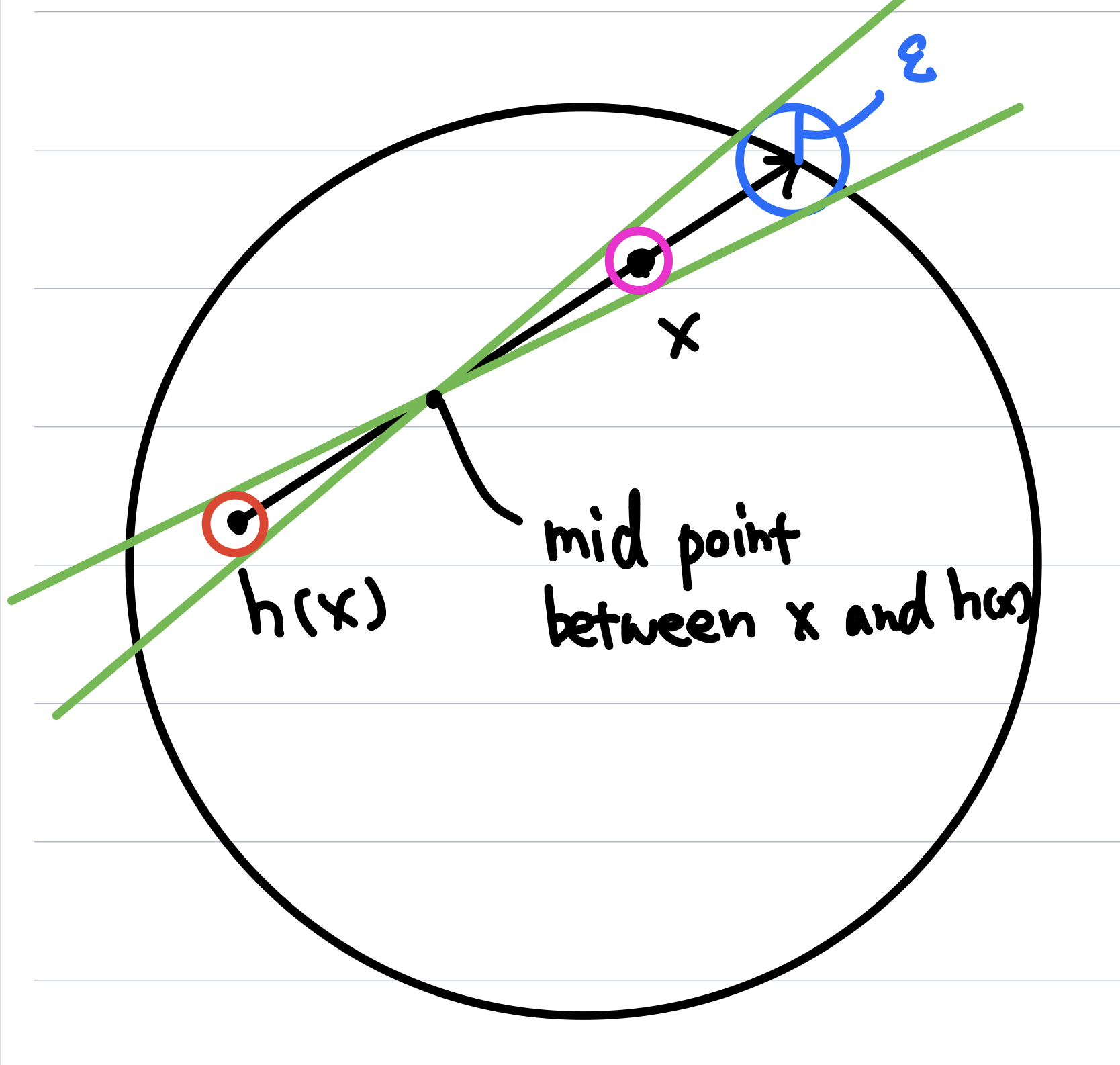
Consider the open ball $N(r(x), \epsilon)$. It is the blue circle in the figure below. Let $m$ denote the midpoint between $x$ and $h(x)$. Then draw all lines that go through both $m$ and $N(r(x), \epsilon)$. That will be the area between the two green lines, excluding the green lines. Let $A$ denote that area.

$A$ is an open subset of $D^2$ and $x, h(x)$ are points in it, so there exist a $c > 0$ such that $N(x, c), N(h(x), c) \subset A$. Since $h$ is continuous, this implies the existence of $c’ > 0$ such that $\abs{x - y} < c’ \implies \abs{h(x) - h(y)} < c$. Let $\delta = \min \{ c, c’ \}$. Then all lines that go through both $N(x, \delta)$ and $N(h(x), \delta)$ go through $N(r(x), \epsilon)$. In other words, if $\abs{x - y} < \delta$, then $\abs{r(x) - r(y)} < \epsilon$. Therefore, $r$ is continuous.

Let $f_0$ be a loop base at $x_0 = (1, 0) \in S^1$, and let $e_{x_0}$ denote the constant loop at $x_0$. Define $f_t = (1 - t)f_0(s) + tx_0$. Then $f_t$ is a homotopy from $f_0$ to $e_{x_0}$ in $D^2$.

Let $g_t(s) = (r \circ f_t)(s)$ for each $t \in I$. We claim that $g_t$ is a homotopy from $f_0$ to $e_{x_0}$ in $S^1$.

• $g_0(s) = (r \circ f_0)(s) = r(f_0(s))$. Since $r$ is the identity function on $S^1$ and $f_0(s) \in S^1$, $r(f_0(s)) = f_0(s)$.
• $g_1(s) = (r \circ f_1)(s) = r(f_1(s)) = r(e_{x_0}(s)) = r(x_0) = x_0 = f_1(x_0)$.
• $g_t(0) = r(f_t(0)) = r(x_0) = x_0$.
• $g_t(1) = r(f_t(1)) = r(x_0) = x_0$.
• The associated map $G(s, t) = g_t(s)$ is continuous since it is a composition of two continuous functions.

Therefore, $f_0 \simeq e_{x_0}$ in $S^1$. Since $f_0$ is any loop based at $x_0$, $\pi_1(S^1, x_0)$ is the trivial group. However, this is a contradiction because $\pi_1(S^1)$ is known to be an infinite cyclic group. Therefore, $h$ must have a fixed point.